
By Ricardo Garcia
The intersection of quantum computation and chemistry
Many problems in chemistry have to do with quantum nature of electrons. Many of the physiochemical properties of compounds can be derived from quantum mechanics descriptions of the electronic structure of a molecule. Complexity observed in biological systems has its origin in quantum mechanics. It is then inevitable to think that the underlying physical device to perform computation on nature must be quantum itself.
In the field of computational chemistry, classical computing has set the bar very high. Overtime physicists and chemists have come with clever simplifications to solve the Schrödinger equation of chemical systems, sacrificing accuracy while remaining efficient. Ab initio quantum chemical calculations must compete with a wide list of competitive alternatives with different levels of accuracy (FF, DFT, Hartree-Fock, coupled-cluster theory) and years of extensive development on CPU and GPU chips.
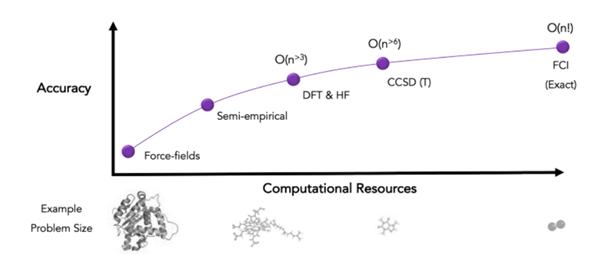
For exact accuracy on a given basis set (Full Configuration Interaction or FCI), just storing the amplitudes of the molecular wave function for a mid-sized molecule requires mindboggling amounts of classical computer memory (exponential scaling in the number of particles that compose these systems). Simulating how they change (their dynamics) in time is even more challenging. For these reasons, the most significant advantage of quantum computing in this realm is making it affordable to solve the Schrödinger equation of correlated electronic wavefunctions for the average computational chemist.
Basics of quantum computation
But before diving into more concrete examples and applications, we briefly describe what quantum computation is all about. Quantum computing is fundamentally different than classical computing because it harnesses the intrinsic subtleties of quantum mechanics.
Quantum computers operate on qubits instead of bits. These may be particles such as electrons with spin up (1), spin down (0) or simultaneously spin up and spin down, a phenomenon called superposition. A small number of qubits can carry an enormous amount of information in a superposition of states. To be precise, a physical system of N qubits can store a superposition of vector states of dimensions. For a more thoughtful discussion on qubit systems, we refer the reader to [1].
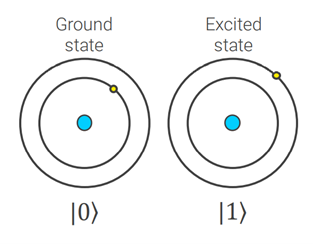
Figure 2: Left) Bloch sphere representation of qubit system. Right) Visual representation of two well-defined states encoded in atomic orbitals.
Certain classes of problems are not amenable for classical computing, such as simulating large quantum mechanical systems and factoring large integer numbers, even out of reach for the world’s fastest supercomputers. For other types of problems, the speedup obtained by quantum computers would be more modest, and, for others, quantum computers are not better than conventional computers.
A common myth about quantum computers is that they could rapidly solve a particularly difficult set of mathematical challenges called NP-complete problems, which even the best existing computers cannot solve quickly (so far it has not been proven) [2]. Quantum computers would supposedly achieve this feat by having hardware capable of processing every possible answer simultaneously. It is important to not get carried away by these superficial explanations and to understand the limitations of quantum computation. There is a whole field dedicated to precisely drawing these boundaries, called computational complexity.
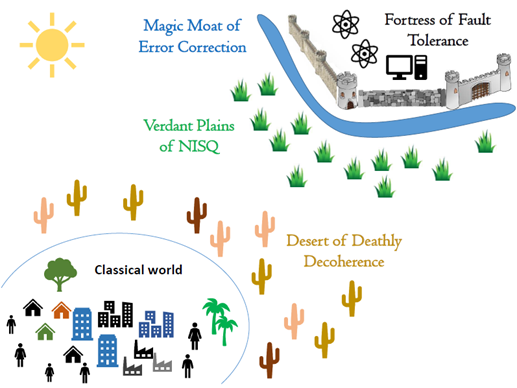
Building a quantum computer is also tremendous engineering challenge. Quantum machines have a significant drawback: they are more error-prone than classical computers. Qubits are extremely fragile and difficult to control, and the slightest environmental disturbance, referred to as “noise,” such as a vibration or change in temperature, results in persistent and relatively high error rates when executing an algorithm. Nonetheless, quantum computers have become more mature than experiments on a physics lab table. As a result, today’s quantum computing devices and those in the near-term future are referred to as Noisy Intermediate Scale Quantum (NISQ). In the longer term, fault tolerance is expected to be achieved with the help of error-correcting schemes, a phase called Fault Tolerant Quantum computer (FTQC).
Opportunities for drug discovery
In this section, we give a short overview of stages of the CADD workflow where QC could have a potential impact and the main quantum algorithms that could enhance the workflow.
Calculating molecular energies is a recurrent task in computational chemistry. Ground state and binding free energy calculations or structural optimizations are common subroutines in many parts of the early drug discovery process, from hit identification to lead optimization. For small and intermediate-sized molecules, the capabilities of classical geometry optimization could provide good enough answers. However, for larger atomistic systems (e.g., protein folding), geometry optimization is a non-trivial task.
Calculating ground energy states along different nuclear positions yields reaction coordinates, which are essential to understanding and predicting chemical reactions and drug synthesis mechanisms. A quantum description of this reactive trajectory is essential for de-novo design.
Another problem of interest in drug design is the computation of the free energy of binding in protein-ligand complexes. In computational screening experiments, molecular docking techniques usually approximate the inter-molecular energy terms of these systems by the usage of empirical or force-field based scoring functions. A full ab initio simulation of the protein-ligand complex is beyond the capabilities of existing classical computers, and docking requires multiple evaluations of this simulation. In lead optimization, molecular dynamics (FEP) or Monte-Carlo sampling are employed to give better estimates of binding affinities, but their high computational cost makes them generally prohibitively expensive for high-throughput screening studies. Thus, by a more accurate and efficient evaluation using scoring functions on QC, the structure-based drug discovery paradigm could substantially benefit.
For ligand-based drug discovery, QSAR models that make use of quantum mechanical descriptors are usually more precise and have higher predictive power. Ideally, QC could serve as an alternative for efficiently calculate these descriptors.
One of the leading quantum algorithms is Quantum Phase Estimation (QPE) that delivers exact energies as FCI methods but with polynomial scaling[3]. Unfortunately, it is unfeasible to implement QPE on near-term quantum hardware due to its long circuit depth and therefore need of a FTQC. An alternative is the Variational Quantum Eigensolver (VQE)[4]. This technique uses a classical optimizer to adjust the parameters of a short quantum circuit towards minimizing a given cost function (e.g., the energy associated with the molecule) iteratively. The first problem instance targeted by the VQE was finding the ground state of helium hydride [5], a simple molecule with a relatively small number of atoms.
Nonetheless, the quest for the first relevant quantum advantage in quantum chemistry is not straightforward. According to [6], the “sweet spot” is between tiny, light atom molecules and large, staggeringly complex multi-metal active sites of protein complexes. However, some caveats challenge the feasibility of VQE in practice. For example, VQE’s iterative nature makes it hard to put bounds on its performance, in terms of running time. Many measurements are needed to accurately estimate molecular energies.
Furthermore, cheminformatics is a field that is more data-driven than ever before. The pharmaceutical industry and academic laboratories are increasingly using and exploring machine learning applications in drug discovery to mine and model the data generated from years of high throughput screening. Quantum machine learning is also a rapidly emerging field exploring how quantum computers can perform machine learning tasks with improved performance over classical computers. Statistical modelling of ADMET properties or de-novo molecular generative models could potentially benefit from QML. Nonetheless, quantum machine learning is still in its infancy and extensive benchmarking is necessary to achieve any kind of empirical quantum advantage, much like deep learning approaches that succeeded with a lot of tinkering and without many theoretical proofs. Additionally, the utility of QML would be much greater if fully error-corrected quantum computers become a reality.
Conclusions
Arguably, we have entered the NISQ era and the first small prototypes of industrially relevant problems in the space of CADD are now being explored. Eventually, with scalable and fault tolerant QC, the power of quantum simulation will enable faster and more accurate characterizations of molecular systems than existing quantum chemistry methods. To fully materialize the potential of QC in drug discovery, the already classical HPC infrastructure must also evolve to co-exist with quantum computing and integrate quantum computational platforms, a key and often underestimated aspect for the success of hybrid quantum-classical workflows.
Given the remarkable achievements in quantum hardware, algorithm development and the recent financial investment boom on the field, there is no reason to believe that this accelerating pace will be slowing down any time soon. Thus, it is foreseeable that academic and industrial R&D in early drug discovery will gradually incorporate quantum computational chemistry platforms into their IT infrastructures within the next decades.
