
By Enric Gibert
In one of my trips to Boston, I found a very good introduction to neural networks and deep learning. The book, whose title is “Deep Learning” from MIT Press being John Kelleher its author, is less than 300 pages long and it is a very pleasant reading during a flight across the Atlantic.
As we have explained in previous posts, Machine Learning is the field of Artificial Intelligence in which algorithms use data to automatically learn and find patterns and relationships. Deep learning, in particular, describes the set of algorithms and techniques in which a neural network with several hidden layers is employed as its core. Although deep learning can be used in unsupervised or reinforcement learning, most of the times it is applied in supervised environments. In supervised learning, a neural network or model is trained with input data (input values) and the expected outputs, and it is iteratively improved until convergence.
The book starts by explaining the basic concepts behind a neuron and a neural network. Although these are mathematical concepts, they are easy to follow and very well presented.
A neuron is a computation unit that performs 2 actions: it computes the weighted sum of its inputs, and it passes this computed value Z through an activation function. The following figure depicts a neuron.
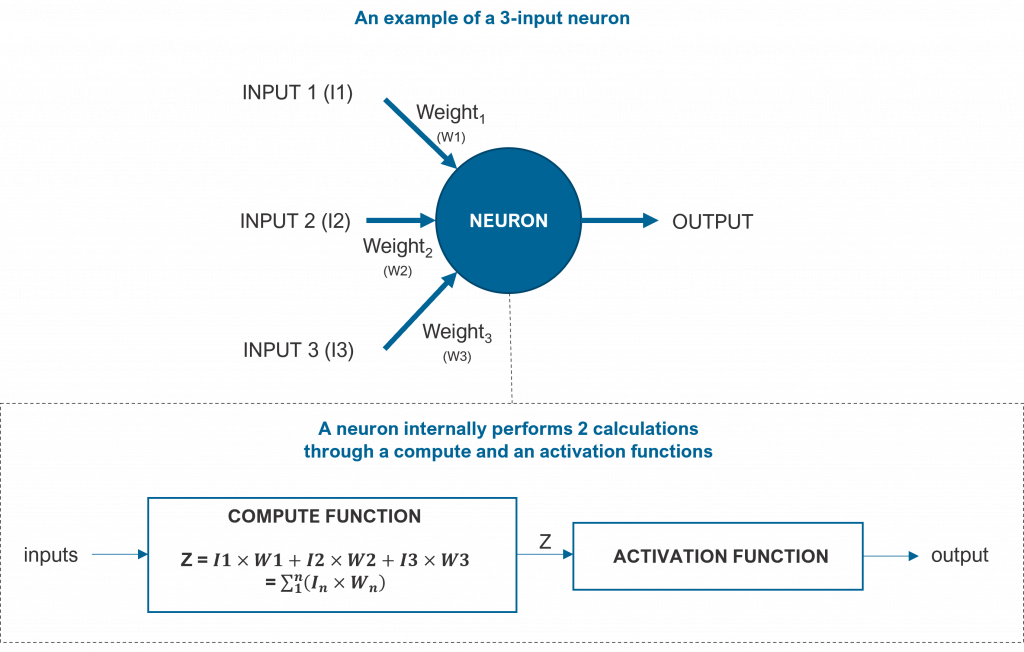
The weighted sum of the input parameters is a straight linear mapping from inputs to outputs following the formula in the previous figure.
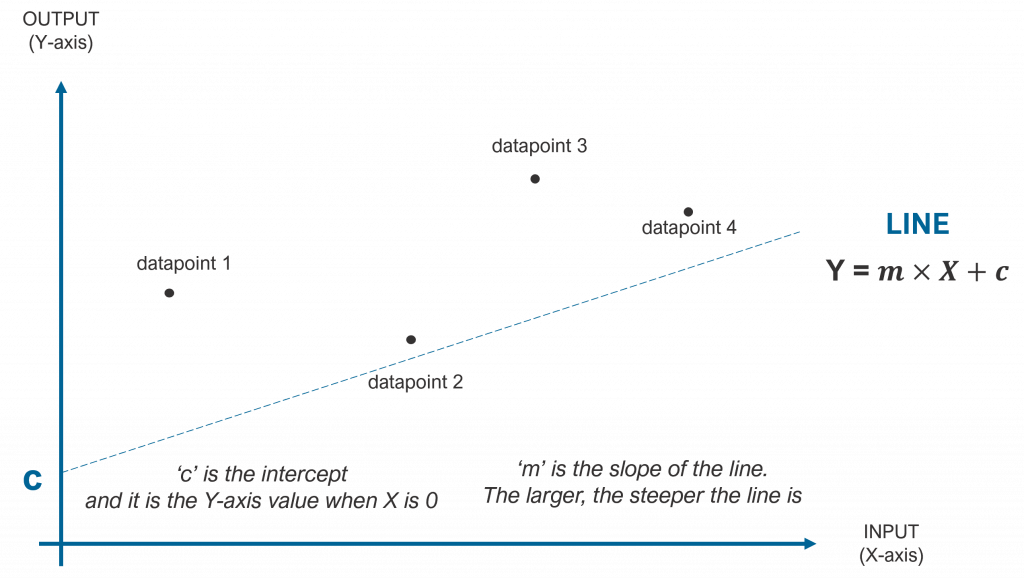
In one dimension (one input), this linear mapping can be plotted as a line as shown below. A plane represents the graphical relationship between two inputs and an output. The book uses these two types of neurons in the examples for simplicity, but in real cases, neurons will have more than two inputs. Although not representable in 3D, one can easily understand the extensions to these multi-dimensional cases.

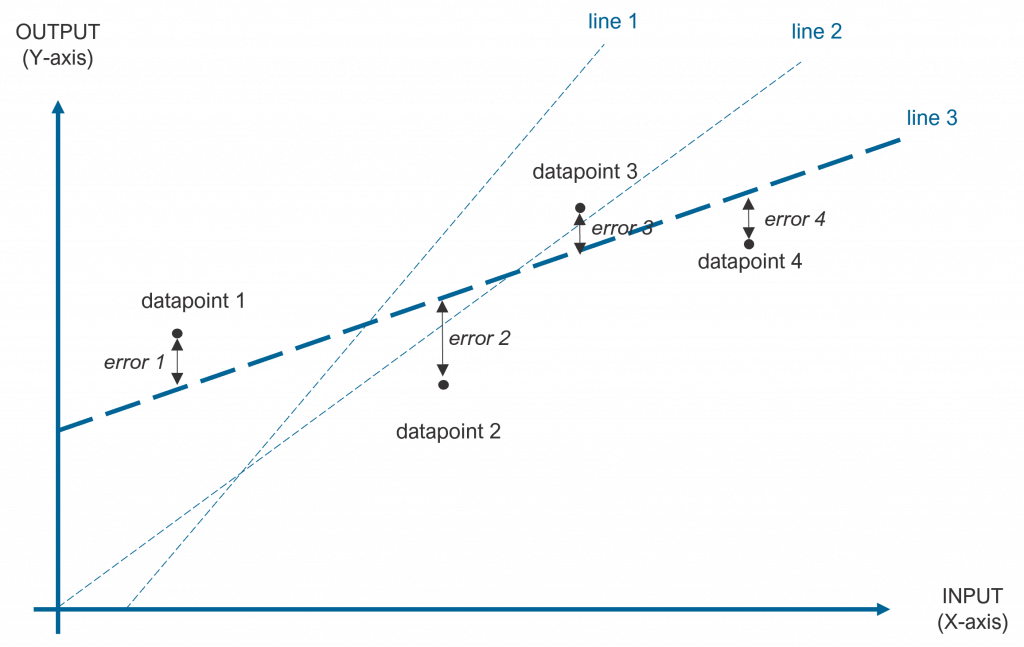
An example of lines trying to match 4 datapoints is shown in the following figure, in which clearly line 3 is the one that best fits the datapoints (the error from the datapoints to the line function that describes them is smaller).
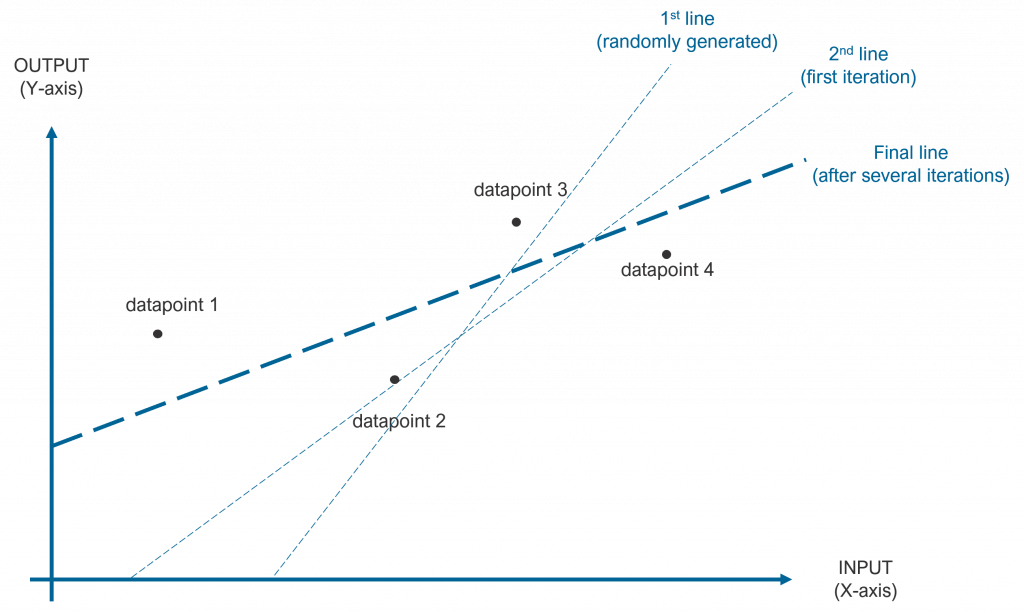
During the training process of a neural network, the weights of the neurons are randomly initialized and iteratively adjusted so that they converge to the expected output, as shown in the figure below. This figure assumes a neural network with one neuron and one input for simplicity. After several iterations, the model should converge to a line like the dark one.
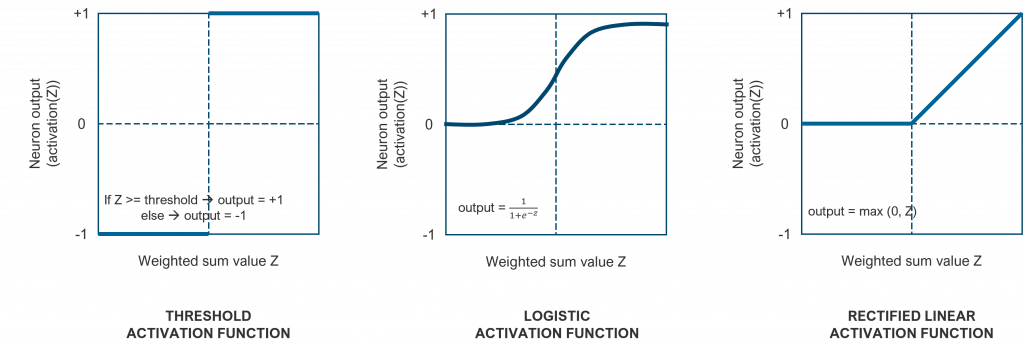
As we have mentioned, once the weighted sum of the inputs is computed, the neuron applies an activation function. The book explains that threshold activation functions were very popular in the early days of neural network research, but they were systematically replaced by logistic functions. Nowadays, rectified linear are the most common activation functions, although this is still a research topic. The following figure shows these 3 types of activation functions.
The reason to use an activation function is to add a non-linear component to the model. In real life, the relationship between inputs and outputs (data correlations) is far more complex than a linear mapping. Even if a neural network may consist of multiple neurons disposed in different layers, the model would still be restricted to a multi-linear mapping. The activation functions of neurons provide this non-linear flexibility.
Once the book has explained the basics of a neuron, it explains several neural network configurations and their evolution.
A neural network is a machine learning model in which several neurons are connected and disposed in different layers. A deep neural network is a neural network with at least, 3 layers (nowadays, it is common to use neural networks with 10-100 layers). Since neural networks are formed by multiple ‘simple’ neurons, we can see that they apply a divide and conquer approach to learning. In the end, each layer / neuron solves a particular and small problem when looking for correlations between inputs and outputs. The following figure shows some neural network configurations.
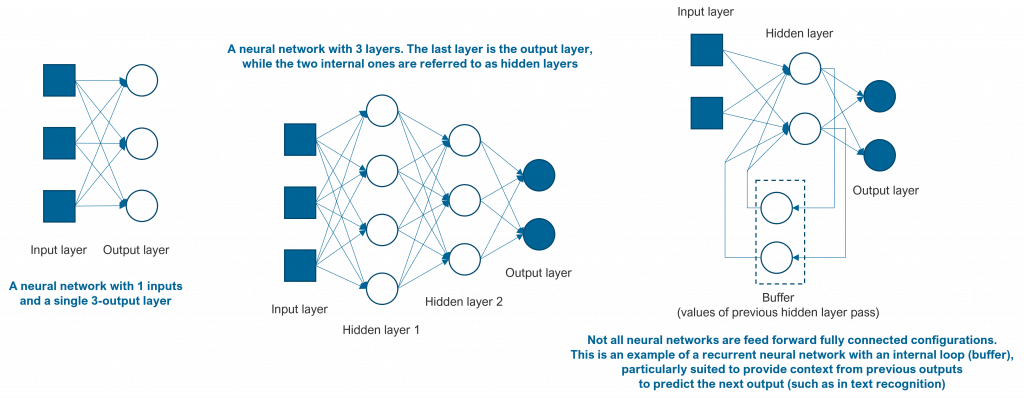
The type and configuration of a neural network is a challenging task. The more complex it is (in number of layers, number of neurons, connections, activation function types, …) the more flexibility it has. However, the more complex it is, the higher chances that it might not converge, or it may take too long to do so. Human intervention is still an important aspect in the design and the implementation of a neural network, starting from the extraction, selection and organization of data to its design, training and deployment. Even though open-source packages such as Scikit Learn are extremely useful and valuable, human expertise still plays a key role.
The main challenge early research had with multiple layer neural networks was the distribution of the error among neurons in multiple layers. Although the book chapter that explains the gradient descent and backpropagation algorithms is the only chapter that requires more mathematical background, their concepts are easy to understand. The author even says that the book can be read without paying too much attention to this chapter if one is confused by the math.
The gradient descent algorithm is the method used to adjust the weights to iteratively converge to the best solution. Given the line example we used before (shown again in the figure below), the gradient descent algorithm iteratively decides how to adjust the ‘c’ parameter of the line equation (the ‘c’ parameter is called the intercept and it is treated as another input to the neuron with a weight of 1 and the ‘m’ parameter of the line equation (the slope).
The partial derivative with respect to each weight is used to update each individually. The idea is that if a weight contributed positively to the error, it will be decreased by a specific amount. If it contributed negatively, it will be increased. The specific value to decrease / increase a weight depends on whether it had a big / small contribution to the error. Note that since this is a multi-parameter optimization problem (even in the case of one input, since a line uses two values / weights, ‘c’ and ‘m’), finding a correct set of weight values is not a one-step process but an iterative one.
On the other hand, the backpropagation algorithm solves the problem of assigning or distributing the error (the blame) among the different layers and different neurons. It was not until this algorithm was proposed that neural networks with hidden layers were not used extensively.
The backpropagation algorithm works in two passes. In the first pass, the forward pass, the current neural network with the current weights is applied and all the weighted sums and activation outputs for each neuron are stored in memory. In the second pass, the backward pass, the error computed for each neuron in the output layer is back propagated or distributed to the previous hidden layer (the last hidden layer) using the different connections and weights among them. The algorithm proceeds by backpropagating these errors to previous hidden layers until the input layer is reached. At that point, each neuron in each layer has been assigned a part of the overall error (part of the blame) and the weights are adjusted by the gradient descent algorithm.
Although neural networks have been studied since the 1940s, its reinvigoration in the last two decades is mainly due to the availability of huge amounts of data (big data in the form of personal pictures, medical images, text in electronic format, digital voice recordings, videos, …) and the availability of specialized hardware. These two factors have boosted the research of more complex and deeper neural networks, leading to new applications and usages. Graphical Processing Units (GPUs) are the most predominant sort of specialized hardware, although there are other options such as Application-Specific Integrated Circuits (ASIC) and Field-Programmable Gate Arrays (FPGA). GPUs are particularly suited for vector and matrix multiplications and initially targeted game graphics. They have lately been applied to other fields that make heavy use of this type of calculations, such as machine learning and cryptocurrencies.
With this post, I hope that I have raised your interest in learning more about neural networks and that you will find the recommended book as a good starting point. You now have a new reading for your next trip across the Atlantic…
